Trying to find math inside everything else

Posts tagged ‘Mathematics’

Habits of Mind, Standards of Practice

For the past three years, I’ve loosely organized my classroom around the Mathematical Habits of Mind which I first read about in grad school at Bard. I would give the students a survey to determine which habits are their strengths and which are their weaknesses, group them so each group have many strengths, and go from there. Last year I even used the habits as the names of some of my learning goals in my grading.

As I was planning for this year and the transition to the Common Core, I was thinking about how to assess and promote the Standards of Practice. And I realized that they are very similar to what I was already doing with the Habits of Mind. In fact, having a habit of mind would often lead to performing a certain practice! In that way, the SoP are actually the benchmarks by which I can determine if the habits of mind are being used.

Let me demonstrate:

Students should be pattern sniffers. This one is fairly straight-forward. SoP7 demands that students look for and make use of structure. What else is structure but patterns? Those patterns are the very fabric of what we explore when we do math, and discovering them is what leads to even greater conclusions.

Students should be experimenters. The article mentions that students should try large or small numbers, vary parameters, record results, etc. But now think about SoP1 – Make Sense of Problems and Persevere in Solving Them. How else do you do that except by experimenting? Especially if we are talking about a real problem and not just an exercise, mathematicians make things concrete and try out things to they can find patterns and make conjectures. It’s only after they have done that that they can move forward with solving a problem. And if they are stuck…they try something else! Experimenting is the best way to persevere.

Students should be describers. There are many ways mathematicians describe what they do, but one of the most is to Attend to Precision (as evidenced in things like the Peanut Butter & Jelly activity, depending on how you do it.) Students should practice saying what they mean in a way that is understandable to everyone listening. Precision is important for a good describer so that everyone listening or reading thinks the same thing. How else to properly share your mathematical thinking?

Students should be tinkerers. Okay, this one is my weakest connection, mostly because I did the other 7 first and these two were left. But maybe that’s mostly because I don’t think SoP5 is all that great. Being a tinkerer, however, is at the heart of mathematics itself. It is the question “What happens when I do this?” Using Tools Strategically is related in that it helps us lever that situation, helping us find out the answer so that we can move on to experimenting and conjecturing.

Students should be inventors. When we tinker and experiment, we discover interesting facts. But those facts remain nothing but interesting until the inventor comes up with a way to use them. Once a student notices a pattern about, saying, what happens whenever they multiply out two terms with the same base but different exponents, they can create a better, faster way of doing it. This is exactly what SoP8 asks.

Students should be visualizers. The article takes care to distinguish between visualizing things that are inherently visual (such as picturing your house) to visualizing a process by creating a visual analog that to process ideas and to clarify their meaning. This process is central to Modeling with Mathematics (SoP4). It is very difficult to model a process algebraically if you cannot see what is going on as variables change. To model, one must first visualize.

Students should be conjecturers. Students need to make conjectures not just from data but from a deeper understanding of the processes involved. SoP3 asks students to construct viable arguments (conjectures) and critique the reasoning of others. Notable, the habit of mind asks that students be able to critique their own reasoning, in order to push it further.

Students should be guessers. Of course, when we talk about guessing as math teachers, we really mean estimating. The difference between the two is a level of reasonableness. We always want to ask “What is too high? What is too low? Take a guess between.” Those guesses give use a great starting point for a problem. But how do you know what is too high? By Reasoning Abstractly and Quantitatively, SoP2. Building that number sense of a reasonable range strengthens our mathematical ability. We need to consider what units are involved and know what the numbers actually mean to do this.

What we do, or practice, as mathematicians is important, but what’s more important is how we go about things, and why. A common problem found in the math class is students not knowing where to begin. But if a student can develop these habits of mind, through practice, that should never be a problem.

Category:

assessment, schooling, theory

Tagged with:

Math Games

Back in January I participated in a panel on Math Games over at the Global Math. I meant to write this follow-up post shortly after, but January was a hell of a month for me and it slipped to the wayside. See my talk here, at the 2:55 mark.

I sorta hit the same point over and over, using six different games as examples, but that’s because I truly believe it is the most important point in both designing math games as well as choosing which games to use in your classroom. If the math action required is separate from the game action performed, then it will seem forced and lead students to believe that math is useless.

Global Math - Math Games.003This can be fine if you want. Maybe you want to play a trivia game, where the knowledge action is separate from the game action. But if you pretend that they are the same, then you have problems.

This is the same essential argument as the one against psuedocontext. It may seem like you could say “It’s just a game,” but students see it as a shallow way to spice something up that can’t stand on its own. (I’m not saying review games and trivia games don’t have their place, but they can’t expand beyond their place.)

Below are the six examples I gave, with the breakdown of their game action and math action. I hope to use what I learned in this process to have us make a new, better math game in the summer, during Twitter Math Camp.

Example 1 – Math Man

A Pac-Man game where you can only eat a certain ghost, depending on the solution to an equation.

Global Math - Math Games.005

If we apply the metric above and think about what is the math action and what is the game action? Here, the math actions are simplifying expressions and adding/subtracting, but the game actions are navigating the maze and avoiding ghosts. If I’m a student playing this game, I want to play Pac-Man. The math here is preventing me from playing the game, not aiding me, which makes me resentful towards that math.

Verdict: Bad

Example 2: Ice Ice Maybe

Global Math - Math Games.008In this game, you help penguins cross a shark filled expanse by placing a platform for them to bounce over. Because of a time limit, you can’t calculate precisely where the platform needs to go, so you need to estimate. That skill is both the math action and the game action, so that alignment means that this game accomplishes its goal.

Verdict: Good

Example 3: Penguin Jump

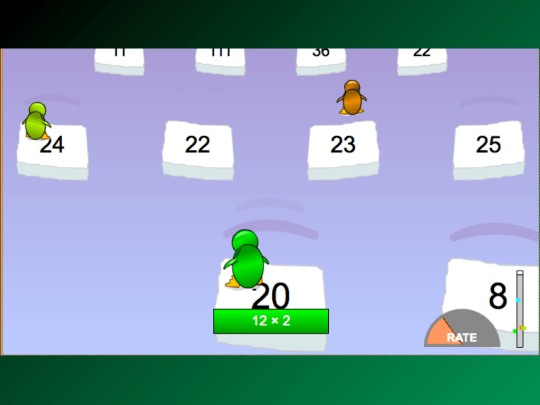Global Math - Math Games.011Here you pick a penguin, color them, and then race other people online jumping from iceberg to iceberg. The problem is that the math action is multiplying, which is not at all the same. The game gets worse, though, because AS the multiplying is preventing you from getting to the next iceberg, because maybe you are not good at it yet, you visibly see the other players pulling ahead, solidifying in your mind that you are bad at math, at exactly the point when you need the most support. A good math game should be easing you into the learning, not penalizing you when you are at your most vulnerable point, the beginning of your learning.

Verdict: Terrible

Example 4: FactortrisGlobal Math - Math Games.014

This is a game that seems like it has potential: given a number, factor that number into a rectangle (shout-out to Fawn Nguyen here in my talk), then drop the block you created by factoring to play Tetris.

Again, the math action is factoring whole numbers and creating visual representations, which are good actions. But the game action is dropping blocks into a space to fill up lines. As Megan called it, though, we have a carrot and stick layout here, and often in many games. Do the math, and you get to play a game afterwards. (Also, the Tetris part doesn’t really pan out, because all the blocks are rectangles, which is the most boring game of Tetris ever.)

Verdict: Bad

Example 5: DragonboxGlobal Math - Math Games.017

I’ve written about Dragonbox before, so I won’t write about it too much here. The goal of Dragonbox is to isolate the Dragon Box by removing extraneous monsters and cards. The math actions include combining inverses to zero-out or one-out, or to isolate variables. The game action is to combine day/night cards to swirl them out, or isolate the dragon box. The game action is in perfect alignment with the math action, which makes the game very engaging and very instructive.

Verdict: Good

Example 6: Totally RadicalPlaying the Root

The board game I created last year (and you can also make your own free following instructions here, or buy at the above link). In this game, the game actions were designed to match up with math actions. Simplifying a radical by moving a root outside the radical sign, as in the picture above, is done by playing the root card outside and removing the square from the inside (and keeping it as points).Global Math - Math Games.021 You also need to identify when a radical is fully simplified, which you do in game actions by slapping the board (because everything is better with slapping) and keeping the cards there as points.

Verdict: Good

Final Note

One of the real challenges of finding good math games, as a teacher, is curriculum. Most math teachers know of several good math games, like Set or Blokus. While these games are great and very mathematical, they’re not the math content that we usually need to teach in our classes. So the challenge falls on us to create our own games, but making good math games is hard. (Making bad ones is pretty easy.) On that note, if you know of some good math games (that meet the criteria mentioned in this post), drop a line in the comments!

 

Category:

games

Tagged with:

No Right Answer

A bit ago I got yelled at by a commenter on Kate’s blog who claimed that being always right is why we like math. The problem with that point of view is that, while yes, you can always be right while doing computation, math isn’t just computation. So the other day I was talking with a friend of mine, and that prompted me to post the following tweets:

My friend Phil (@albrecht_letao) responded to the question, and he came up with an answer of $20/hr. When I worked it out with my friend, we came up with $14.25. Does that mean one of us is wrong, since we got different numbers?

No, of course not. What happened is we approached the problems in different ways. Phil only calculated the monetary value: with his amount, my friend would earn the same amount of money she does now. He figured this was an important way to look at it, for paying bills and whatnot. Our calculation came from thinking about how her time is being compensated. Since those 16 hours are being wasted (she has to work them for free; actually, she pays to lose that time), we calculated her “real” hourly rate and used that.

There can be more answers than even these two, depending on what you think is important. But it’s a clear example of a problem, solved using math, with no one right answer. That’s what math is about. I tweeted it thinking maybe it could be a problem worth considering in class, to show that essential idea to students.

What do you think?

P.S. The right answer, of course, came from @calcdave:

 

Category:

anywhere, math

Tagged with:

Algebra Taboo

I remember reading about the idea of Math Taboo on Sam Shah’s blog, this post by Bowman Dickson. I feel like I had the idea independently, but it seems like many people have, by doing a cursory Google search of the phrase.

Unfortunately, there are lots of posts ABOUT math taboo, but no real materials provided. If I have seen anything, it’s a lesson plan on having the students make their own. Or I saw one for sale, but it was for the elementary level. So I made one myself.

My co-teacher and I went through all the Integrated Algebra regents given since 2008 and pulled out any words that it’s possible a student might not know. I also went through my own lessons and pulled out any vocabulary I had given them. Below is the .pdf for printing your own (I used card stock and laminated), and two .doc templates if you’d like to make more, or alter the ones I have. I made a total of 126 cards (63 double sides – maybe slightly overboard).

Since I found no others, it makes sense to share.

Downloads

Math Taboo (full pdf)

Math Taboo Pink  Math Taboo Blue (doc template)

Category:

games, lessons, math

Tagged with:

Egyptian Fractions

As I stated earlier, I’ve been trying hard this to integrate the other subjects more into my math lessons (and the other teachers are happy to work vice versa, because I’m on a great grade team). This process is made easier by actually having a Special Ed co-teacher for one section, and she specializes in math (and sees every subject, so can comment on all of them). So my first lesson explicitly tying history to math just went off, a lesson on Egyptian Fractions.

My goal for this lesson was really to get some fraction practice in while still learning something new, while also highlighting the “symbol that represents the multiplicative inverse,” , which I’d tie in on the next lesson about exponents (aka an exponent of -1). We worried, though, that the translation process would be too tough while dealing with fractions. That’s when we came up with this:

The Fraction Board has 60 square on it (which will be good reference for when I deal with sexagesimal Mesopotamian numbers soon), so each piece is cut to fit the amount of square that will cover that fraction of the board. To make the boards, I just made a 6×10 table in word as square-like as I could, printed on card stock. Then I cut the pieces out of the extra boards and had slave labor student volunteers color them in for me.

Each fraction have multiple pieces to represent the different ways you can fit them. (For example, 1/2 is 30 square, so I have a 3 x 10 piece and a 5 x 6 piece). But each fraction is also colored the same, because in Egyptian Fractions you can only use one of each unit fraction.

Then I would put up a slide like this on the board:

And the students would have to make that shape on their boards, with no overlapping and only using each color once. For the first one I shared a possible solution:

But I got really excited when the students could come up with multiple different solutions for each problem. And I would increase the difficulty of each one, until I would just get to a fraction with no picture:

And they still nailed it. Eventually I would move away from the boards and show the process of how to do it without the boards. We’d do some simultaneous calculation (using the greedy algorithm or more natural intuition) and checking on the board. Then we’d try with non-sexagesimal fractions. And every time we would translate our answers into hieroglyphics as well. So by the end of the lesson they could work on a worksheet where I just gave a fraction and they gave me hieroglyphics in return. (Not all of them could do this completely, but most could do some of the sheet). I think, overall, it went pretty well.

Egyptian Fraction Slides (Powerpoint)

Egyptian Fractions Slides (pdf)

(WordPress doesn’t seem like it’ll host my slides in their original Keynote form. That’s bothersome.)

Category:

history, lessons, math

Tagged with:

It All Fits Together

One of the best things about being a math teacher, as opposed to a mathematician, is that because I have to think about how to explain a concept to people who don’t get it, I have to think about concepts in different ways than I ever have before. So I often make connections that maybe I should have already made, but hadn’t, and I see the beauty of the conventions and connections of mathematics.

 

Today I was musing about the use of -1 as an exponent to give us a reciprocal, because my next lesson is about Egyptian Fractions, and so their fractions are basically the number with an inverse symbol, which we still use, -1. And then I thought, well, yes, that is our inverse symbol, for functions too. Of course, that makes sense. But the clearness and uniformity of it seemed new. So often we learn about things in math in such disconnected ways, so it’s just “Here’s one use for the -1. Here’s another. That’s the way we do it.” But not why it’s the same for both.

 

And I get these realizations all the time. At least 5 last year. (I think another I had had to do with FOIL.) I hope I keep getting them. But the next step is, of course, to figure out how to let the students get them. Because then, I think, they won’t hate math so much.

Category:

math

Tagged with:

Math is like…

So on the first day of math class, I gave the students this little analogy:

“Math is like cooking. You don’t need to know how to do it to live your life, but if you don’t you need to always rely on someone else to do it for you, and it will wind up costing you more money. Most people know how to do the very basics, enough to get by, but those who really understand the concept make their lives richer and more enjoyable on a daily basis.”

I also told them math was like a language, a pretty familiar analogy. But then I asked them to come up with their own, and they created a poster based on the different answers.

Here’s some they said:

“Math is like your parents: sometimes you just don’t understand them, but they’re just trying to look out for you.”

“Math is like a wave: sometimes it’s big, sometimes it’s small, but it never stops.”

“Math is like the subway: you can read the map and think you know where to go, but you don’t really know until you’re there.”

“Math is like time: there’s a new number every second.”

“Math is like climbing a mountain: it’s really hard, but you feel great when you get to the top.”

“Math is like HIV: it never goes away.”

Category:

student response

Tagged with: