Trying to find math inside everything else

Posts tagged ‘desmos’

Streak Bonus in the Pokémon TCG

Here’s a fun problem I worked on recently – fun enough that I nerdsniped two of my coworkers about it. Here’s the problem:


In the Pokémon TCG Pocket app, I would earn 10 points for winning a match and lose 7 points when losing a match. However, you also get a win streak bonus – the second win in a row gets a bonus of 3 points, the third gets 6, the fourth 9, and the fifth (and all subsequent) gets 12. Assuming I have a win rate of 50% (which I did at the time), what’s my expected value for playing n games? (How many games would I expect to play to earn x points?)

Below is a journey through my thought process – you can jump to the end if you just want the answer.

I started by writing out the different possibilities of runs of wins and losses for 1 game, 2 games, 3, etc. Thinking that if I listed them by hand I might miss some, I realized that I could use CONCATENATE in a spreadsheet to work recursively – take all the runs from (n-1) games and append a W at the end, then repeat the process with an L. So I did that here:

https://docs.google.com/spreadsheets/d/1izBy3wN-sVFV8SxExDxGC9rNVebEA5C7iPydU_kmP1Y/edit?gid=748567562#gid=748567562

(There’s 3 tiers, each with its own sheet – Master Ball Tier, where you lose 10 points on a loss, Ultra Ball with 7 [the tier I’m in], and Great Ball with 5. It makes sense to work through the problem in Master Ball, so you can just focus on the streak, and then adjust afterwards.)

Notably because I had some errors in my data, my calculated EVs and EV/game didn’t seem like nice numbers, so my first instinct was to turn to statistics. I did a log regression for the EV/game numbers and then used that to calculate when I would hit the number of points I needed (340). [You can just change which function it is to change tiers.]

https://www.desmos.com/calculator/tspirmvama

This felt unsatisfactory and I wondered if my logic was sound, so I roped in the inimitable Sam Shah and talked him through the problem. He voiced his belief that there would be an explicit solution, so that turned me back to my table. As I walked him through it, we found the errors I had, which made things look nicer, so on the right track.

What really matters as you go through each game in the run, once you get past 5 games, is just the final five games. As you go through each game, we’ll notice that there’s a doubling happening. For example, after 2 games there’s 1 way to end in 2 wins, 1 way to end in 1 win, and 2 ways to end in a loss. After 3 games, there’s 1 way to end in 3 wins, 1 way to end in 2 wins, 2 ways to end in 1 win, and 4 ways to end in a loss. Once you get past 5 games, you no longer need to be introducing new sequences to look for, so then they start combining, as below:

For every game that represents a run that ends in 5 wins, I need to add 22 points. For every game that represents a run that ends in 4 wins, I need to add 19 points. And so on. And the total number of possible runs is 2^n, so to get the expected value of a single game, I would need this expression (for Ultra Ball tier):

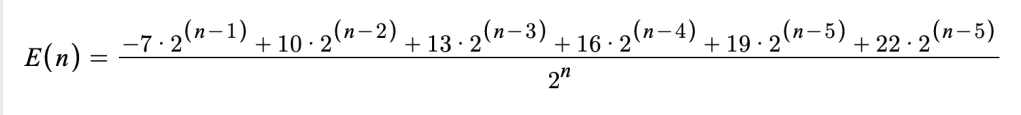
Then I just need to add that value for every game past 5 onto the value I already calculated for 5 games, and voila!

But wait, you may have noticed that that expression could be reduced. In fact, once you reduce it, it no longer depends on the variable n – it’s constant!

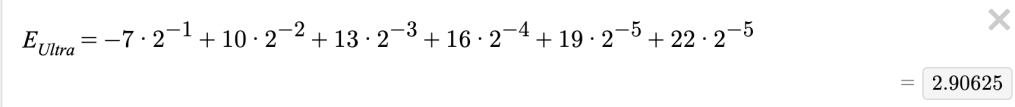
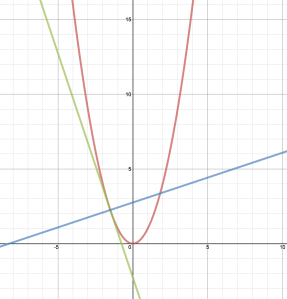
So basically we have linear function with this value as the slope (and a domain of more than 5 games). So I made this graph to represent the three tiers – just input for y how many points you’ll need and the x-value for each intersection will tell you how many games you expect to play for each tier.

https://www.desmos.com/calculator/jdrc6qzrsh

Extension questions: What if I didn’t have a 50% win rate? How low could my win rate go and still have a positive expected value? I leave those as an exercise to the reader.

Category:

analysis, games, joy

Tagged with:

Parallel to a Parabola?

A while back, I was working on a lesson about average rate of change and wondered the following question: “Could you use the word ‘parallel ‘to describe two non-linear functions that have the same rate of change/don’t intersect?”

Screen shot 2014-06-18 at 8.53.48 AM

Jonathan’s response, though, made me think about what it actually means to be parallel. Often when you ask students, they will respond “two lines that never intersect,” which I usually push back against because 1) how do you know they never ever intersect? and b) skew lines never intersect, either. So when I explain parallel lines, I use the fact that they have the same slope/go in the same direction as the actual definition, which has the consequence of never intersecting. So I looked it up on Wikipedia.

Given straight lines l and m, the following descriptions of line m equivalently define it as parallel to line l in Euclidean space:

  1. Every point on line m is located at exactly the same minimum distance from line l (equidistant lines).
  2. Line m is on the same plane as line l but does not intersect l (even assuming that lines extend to infinity in either direction).
  3. Lines m and l are both intersected by a third straight line (a transversal) in the same plane, and the corresponding angles of intersection with the transversal are congruent. (This is equivalent to Euclid‘s parallel postulate.)

I don’t think statement 3 was particularly useful to me, but the idea of being equidistant was interesting. A vertically shifted parabola is not equidistant from the original – though they never touch, the distance between them gets smaller and smaller.

So that raised the next question – how do I actually measure the distance between two parabolas at a given point? I asked my boyfriend and he responded, “Well, you definitely need calculus….” And who better to swoop in and help with that than Sam Shah.

Screen shot 2014-06-18 at 8.54.01 AM

So now that I know how to find the minimum distance between two functions, all I need to do is find a function that whose minimum distance to my original function is constant, and then I should have something that you could call parallel.

I made a little Desmos graphs with sliders, to help me visualize the process (click to access):

Screen shot 2014-06-21 at 1.27.13 PM

So I have the equation of the perpendicular line

y = \frac{-1}{f'(a)}(x-a)+f(a)

But that wasn’t really helping me see what the parallel function would actually look like. So then I turned to Geogebra. I needed to make a point on the perpendicular line that was a certain distance away from the function, say a distance of 1. So to figure out the coordinates of that point (x,y), I just used the distance formula, plugging in y from above.:

\sqrt{(x-a)^2+([\frac{-1}{f'(a)}(x-a)+f(a)] - f(a))^2} = 1

That gave me the coordinates of the point that is a distance of 1 away from f(x) at a:

(a + \frac{f'(a)}{\sqrt{1+(f'(a))^2}},\frac{-1}{\sqrt{1+(f'(a))^2}}+f(a))

So I made that point in Geogebra and activated the trace, which gave me this:

Screen shot 2014-06-21 at 2.20.38 PM

Lastly, I thought, well, what exactly is this function that I’ve traced? It looks kinda quartic, but that can’t be, because any quartic like this would intersect the parabola, right? So I tried to write the function for it, using parametric equations. Using f(t) = t^2, I made the parametric equation (t + \frac{2t}{\sqrt{1+4t^2}},\frac{-1}{\sqrt{1+4t^2}}+t^2).

I tried to plug that into Wolfram-Alpha to get the closed form, but it was a mess, so I still don’t really know what the closed form would look like. But who says a parametric form isn’t a solution?

(Here is a Desmos page with a summary of what I’ve done, and some sliders to play with, similar to the Geogebratube page, but with colors.)

Category:

math

Tagged with: