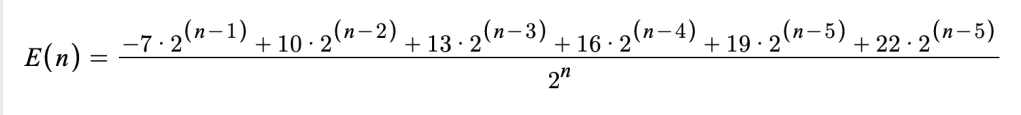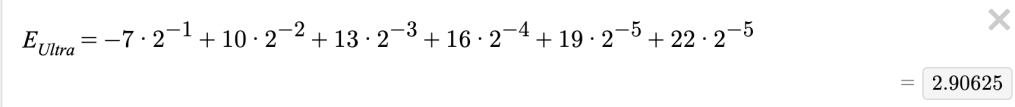Discrete Math & Democracy, Weeks 5-6
This time I did purposefully combine two weeks – we had 3 days of no class between them, with the PSAT, a PD day, and a holiday.
We started week 5 with another quiz – they asked for this one to be on paper instead of on the computer, and who was I to go against the will of the people? So below is the quiz I gave:
At this point we wanted to finish off our chart of Methods vs Criteria (except for IIA).
We were able to explain the whether most of the methods passed or failed Condorcet and Anti-Condorcet logically or with a counterexample, but the proof that the Borda Count passes Anti-Condorcet is a little more subtle, and a little more algebraic, so I broke that out into a worksheet.
This led to a good combinatorics connection for me. The standard way to calculate the Borda Count is to assign points based on how many candidates you beat, so if you look at it from the point of view of a ballot, in an election of 5 candidates, e.g., a single ballot gives out 4 + 3 + 2 +1 + 0 = 10 points. But another way to view the Borda Count is that you earn a point from a candidate (as opposed to from the voter/ballot) every time you beat them in a 1v1 match. Well, with 5 candidates, how many possible 1v1 matches are there? 5C2 = 10. Oh wait, that’s the same as before! And shows why the C2 column of the Arithmetic Triangle (sometimes known as Pascal’s) is the Triangle Numbers.
Speaking of combinatorics, the next part was fun. First, we considered how many different ways there are to seed an 8 person tournament. There’s lots of ways to represent this number – my first conception of it involved double factorials!! (Sam was shocked I had found a natural use for double factorials.) Thought the final conception was came up with (n! / 2^k, where k is the number of symmetries in the bracket) was easier to calculate and made more sense.
But the real fun part was thinking, well, if there’s 315 different ways to seed the bracket, is there a way to seed it such that every person can win? So I challenged them to seed the tournament so that A wins, and then so that C wins. (Some candidates couldn’t win, like B and D, because they had fewer wins than the number of matches in the tournament. A and C were possible but harder because they had few paths to victory.)
After this I introduced the concept of a Condorcet method, which tournaments are, despite their manipulability flaw. So I expanded our chart to include the methods we’d be doing soon: Copeland’s, Minimax, Nanson, and Ranked Pairs.
Finally, we had another quiz: